WAEC Further Mathematics Questions and Answers 2025 is online. Check it below.
Have seen the WAEC Further Mathematics Questions and Answers for the 2025 May/June WAEC Examination? If you have not and you would like to have full access to it, all you have to do is read this article carefully to the end.
When it comes to WAEC Further Mathematics examination, candidates are faced with pressure owing to the fact that that the subject is usually seen as one of the difficult subjects. However, if candidates would granted access to the expected questions and answers for every year, there is going be great improvement when the 2025 WAEC Result will be released.
In this article, I am going be releasing some some EXPO on 2025 WAEC Further Mathematics Questions and Answers for both Essay and Objective. If you desire to get more detailed information, make sure you continue reading article.
See Also: Updated May/June WAEC timetable for 2025 | Nigeria, Ghana, Gambia, Sierra Leone & Liberia
WAEC Further Maths 2025:
1- 10: DCCBBCACBA
11-20: BACABCCCDC
21-30: CACDCAABCB
31-40: CBBDDDADAD
WAEC Further Maths Questions and Answers
These answers are for 2025 WAEC Further Maths examination. Keep moving to the next section for more correct answer to the questions.
Question 1

Question 2
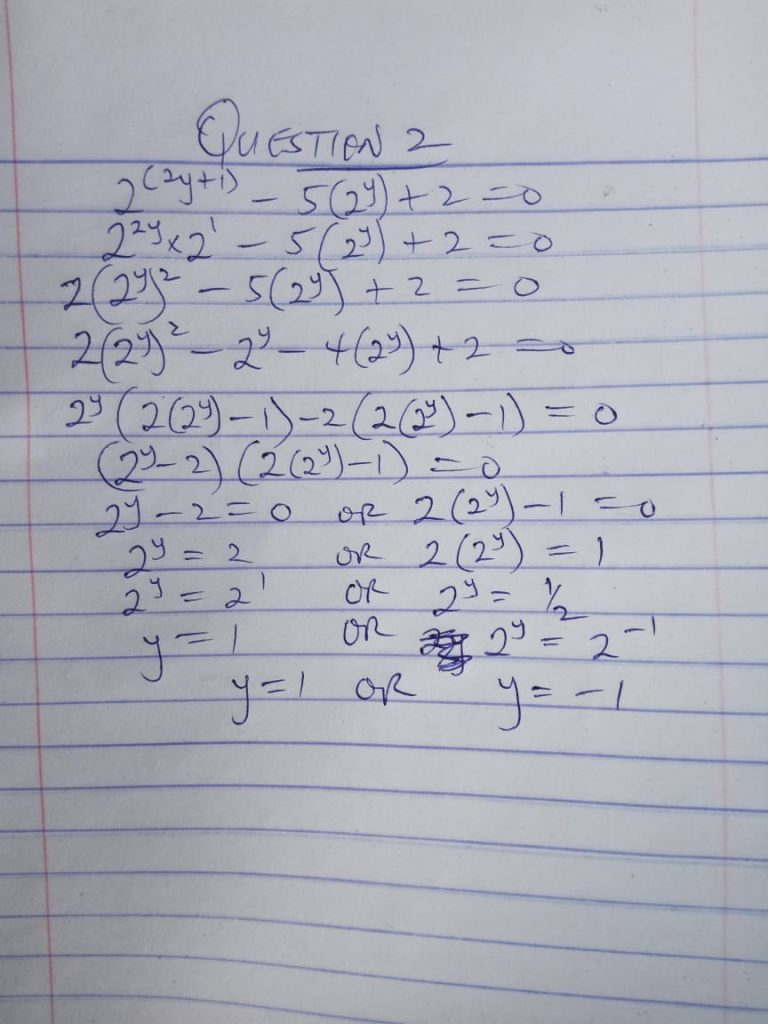
Question 3

Question 4
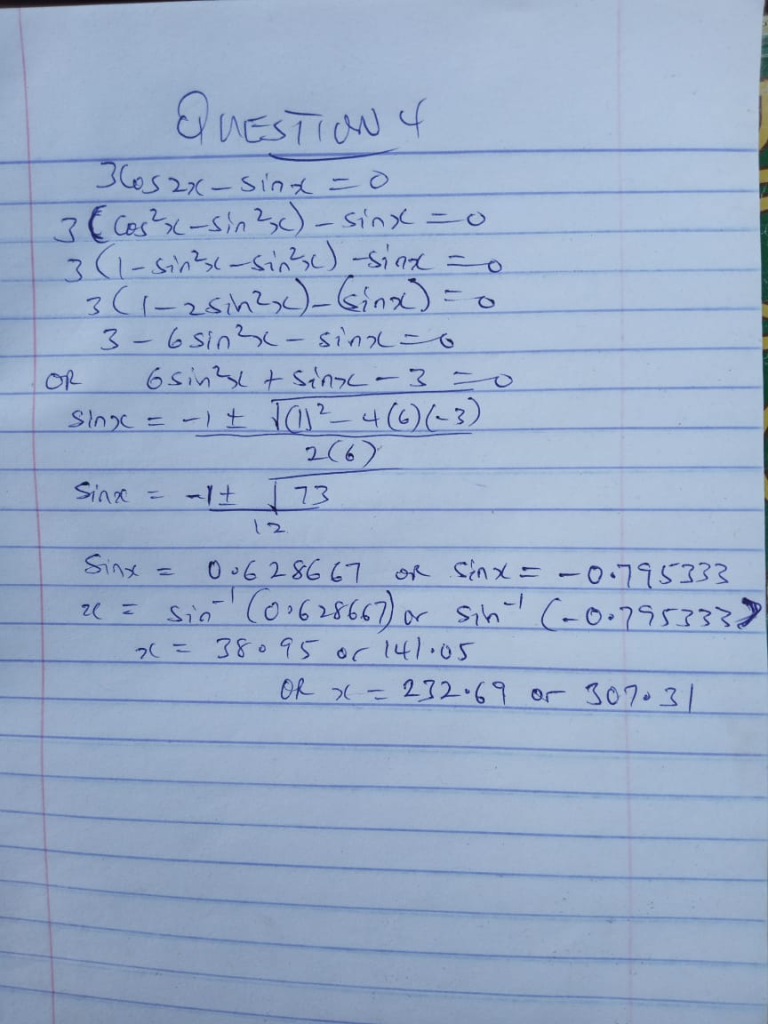
Question 5:
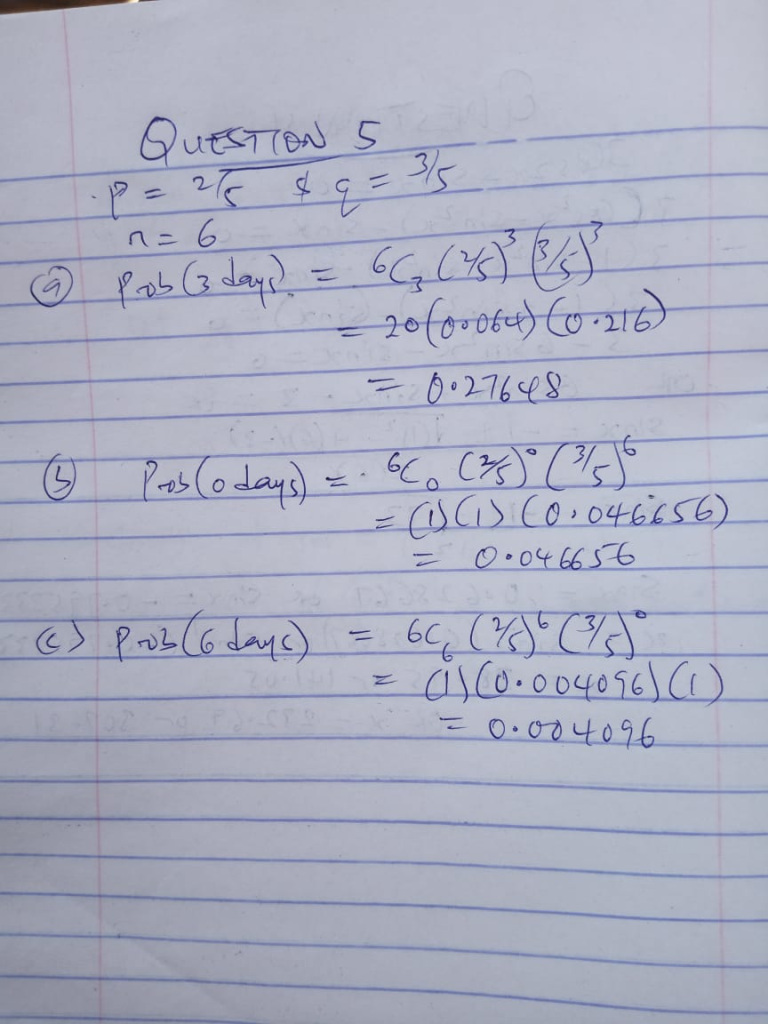
Question 6:
Question 7:
Question 8:

Question 10:
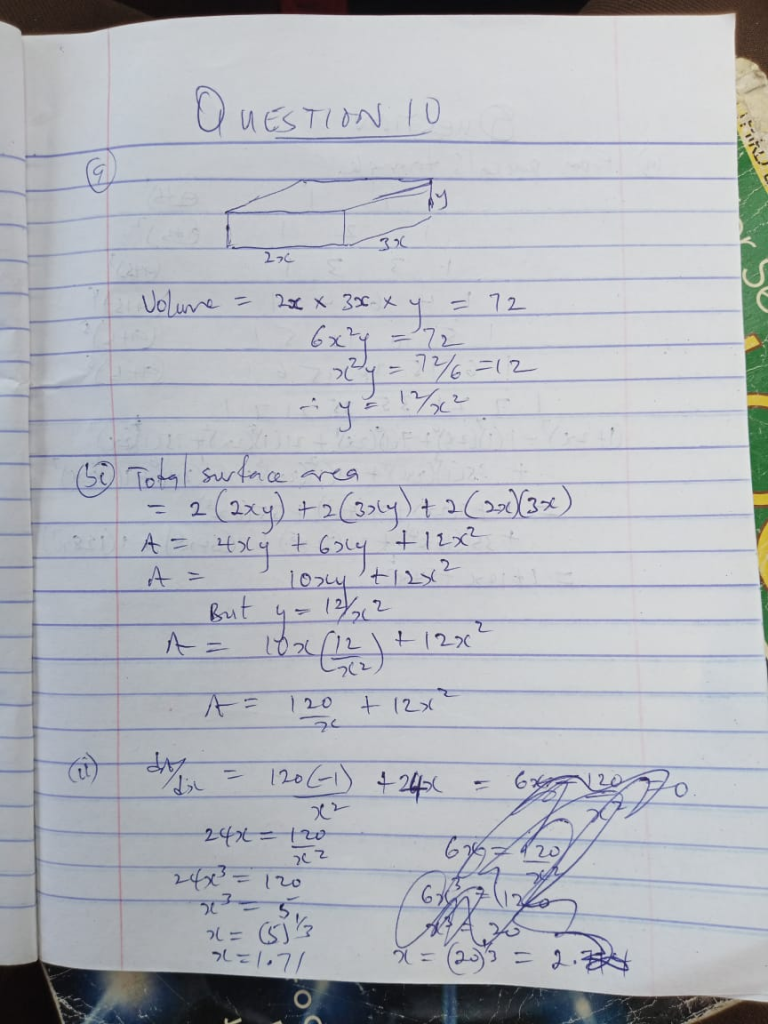
Question 11:
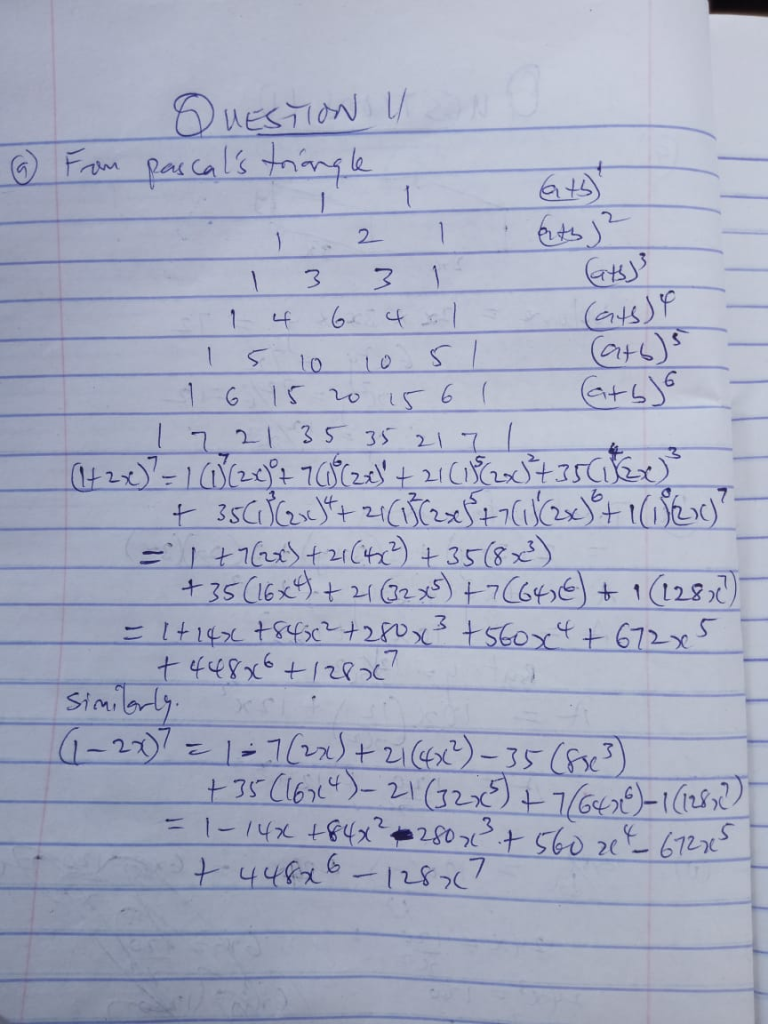
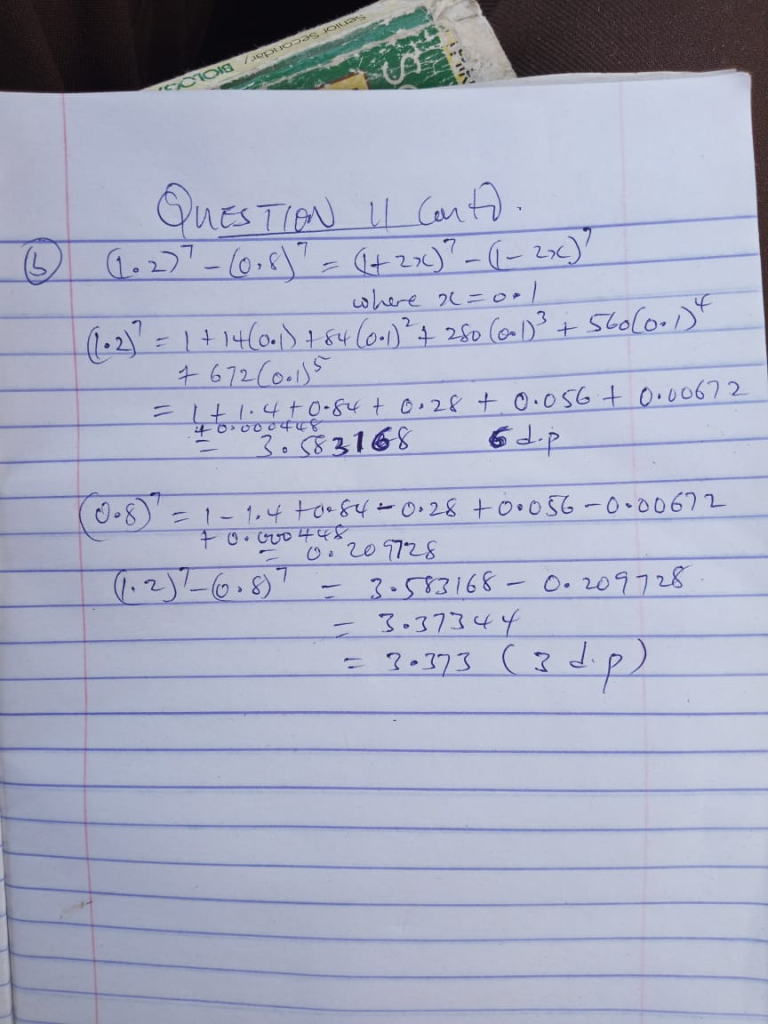
Question 12:

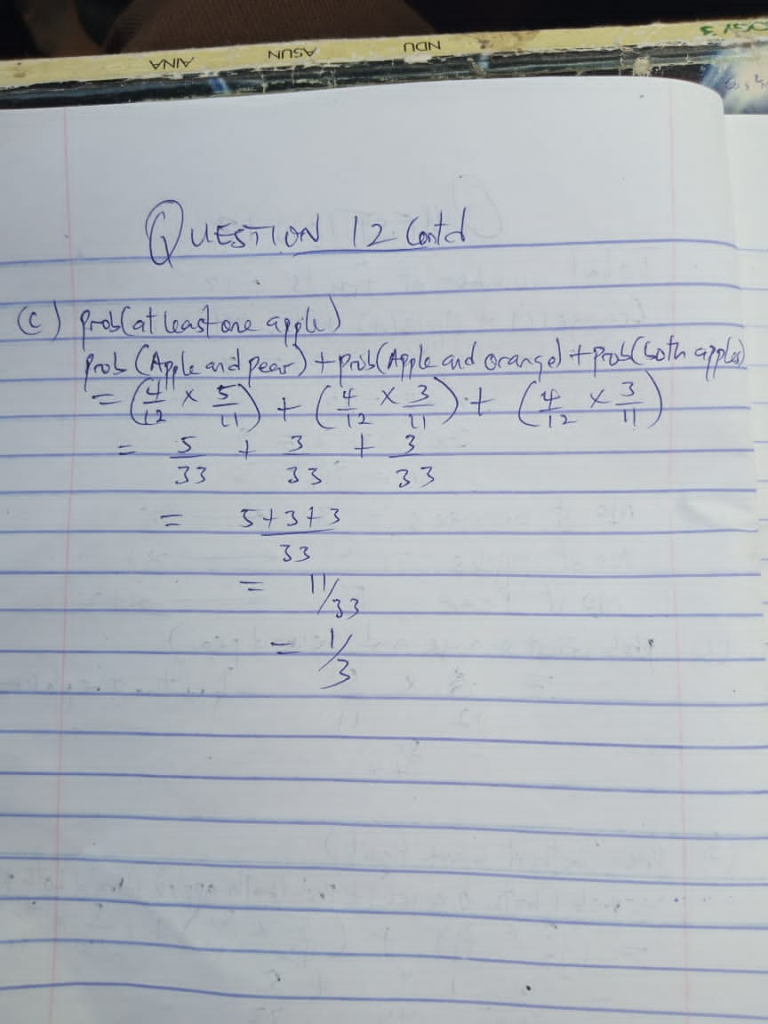
Question 14:


Given:
f(x)={(4x-x^2)dx
f(x)=2x^2 – x^3/3 + K
f(3)=2(3)^2 – (3)^2/3 + K =21
18 – 9 + K=11
9+K=21
K=21-9
K=12
Therefore
f(x)= -x^3 + 2x^2 + 12
2025 Further Mathematics Objective Questions and Answers
The following are the exact WAEC Further Mathematics Objective Questions for 2024 examination:
1. A binary operation ∆ is defined on the set of real numbers R, by x∆y = √x+y−xy/4, where x, yER. Find the value of 4∆3
- A. 16
- B. 8
- C. 4
- D. 2
- Correct Answer: Option D
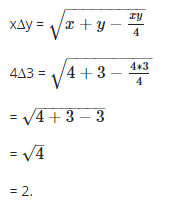
2. (3√6/√5+√54/3√) −1
- A. 5√3/6
- B. 3√15/6
- C. 5√6/12
- D. 5√3/123
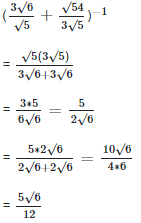
Correct Answer: Option C
3. If log10(3x+1)+log104 = log10(9x+2), find the value of x
- A. 1/3
- B. 1
- C. 2
- D. 3
- Correct Answer: Option C
4. Simplify 9∗3n+1−3n+2/3n+1−3n
- A. 3
- B. 9
- C. 27
- D. 815
- Correct Answer: Option B
5. Consider the following statement:
x: All wrestlers are strong
y: Some wresters are not weightlifters.
Which of the following is a valid conclusion?
- A. All strong wrestlers are weightlifters
- B. Some strong wrestlers are not weightlifters
- C. Some weak wrestlers are weightlifters
- D. All weightlifters are wrestlers
- Correct Answer: Option B
6. The functions f:x → 2x2 + 3x -7 and g:x →5x2 + 7x – 6 are defined on the set of real numbers, R. Find the values of x for which 3f(x) = g(x).
- A. x = -3 or -5
- B. x = -3 or 5
- C. x = 3 or -5
- D. x = 3 or 5

Correct Answer: Option C
7. Express 4π/2 radians in degrees.
- A. 288º
- B. 200º
- C. 144º
- D. 120º8
- Correct Answer: Option C
8. A straight line makes intercepts of -3 and 2 on the x and y axes respectively. Find the equation of the line.
- A. 2x + 3y + 6 = 0
- B. 3x – 2y – 6 = 0
- C. -3x 2y – 6 = 0
- D. -2x + 3y – 6 = 0
- Correct Answer: Option D
9. Which of the following is the semi-interquartile range of a distribution?
- A. Mode – Median
- B. Highest score – Lowest score
- C. 1/2 (Upper Quartile – Median)
- D. 1/2 (Upper Quartile – Lower Quartile)10
- Correct Answer: Option D
10. Evaluate ∫0−1 (x + 1)(x – 2) dx
- A. 7/6
- B. 5/6
- C. -5/6
- D. -7/6
- Correct Answer: Option D
Check: WAEC Literature Questions and Answers 2025 | Novels, Essay & Objective
11. If 36, p, 9/4 and q are consecutive terms of an exponential sequence (G.P), find the sum of p and q.
- A. 9/16
- B. 81/16
- C. 9
- D. 9⁹/16
- Correct Answer: Option D
12. Differentiate (5x3+x2)/x, x ≠ 0 with respect to x.
- A. 10x + 1
- B. 10x + 2
- C. x(15x + 1)
- D. x(15x + 2)13
- Correct Answer: Option A
13. Given that 8x+m/x2−3x−4 ≡ 5/x+1 + 3/x−4
- A. 23
- B. 17
- C. -17
- D. 17
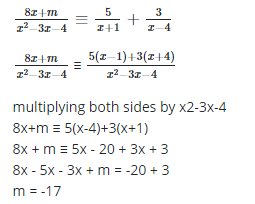
Correct Answer: Option C
14. If x2+y2+−2x−6y+5=0, evaluate dy/dx when x=3 and y=2.
- A. 2
- B. -2
- C. -4
- D. 415
- Correct Answer: Option A
15. Evaluate 1∫0 x2(x3+2)3
- A. 56/12
- B. 65/12
- C. 12
- D. 65
- Correct Answer: Option B
See Also: WAEC Geography Questions And Answers 2025 | Essay & Objective
16.
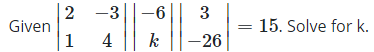
- A. -8
- B. -5
- C. -4
- D. -317
- Correct Answer: Option B
17. A linear transformation T is defined by T: (x,y) → (3x – y, x + 4y). Find the image of (2, -1) under T.
- A. (7, -2)
- B. (5, -2)
- C. (-2, 7)
- D. (-7, 2)18
- Correct Answer: Option A
18. Evaluate 4p2+4C2−4p3
- A. 18
- B. 6
- C. -6
- D. -18
- Correct Answer: Option C
19. Find the coefficient of x2 in the binomial expansion of (x+2/x2)5
- A. 10
- B. 40
- C. 32
- D. 8020
- Correct Answer: Option A
20. Given that P = {x: x is a multiple of 5}, Q = {x: x is a multiple of 3} and R = {x: x is an odd number} are subsets of μ = {x: 20 ≤ x ≤ 35}, (P⋃Q)∩R.
- A. {20, 21, 25, 30, 33}
- B. {21, 25, 27, 33, 35}
- C. {20, 21, 25, 27, 33, 35}
- D. {21, 25, 27, 30, 33, 35}
- Correct Answer: Option B
21. A particle moving with a velocity of 5m/s accelerates at 2m/s2. Find the distance it covers in 4 seconds.
- A. 16m
- B. 26m
- C. 36m
- D. 46m
- Correct Answer: Option C
22. If Un = kn2 + pn, U1 = -1, U5 = 15, find the values of k and p.
- A. k = -1, p = 2
- B. k = -1, p = -2
- C. k = 1, p = -2
- D. k = 1, p = 2
- Correct Answer: Option C
23. In how many ways can six persons be paired?
- A. 5
- B. 10
- C. 15
- D. 20
- Correct Answer: Option C
24. Solve: 32x−2 − 28(3x−2) + 3 = 0
- A. x = -2 or x = 1
- B. x = 0 or x = -3
- C. x = 2 or x = 1
- D. x = 0 or x = 325
- Correct Answer: Option D
25. Given that P = (-4, -5) and Q = (2,3), express →PQ in the form (k,θ). where k is the magnitude and θ the bearing.
- A. (10 units, 053º)
- B. (9 units, 049º)
- C. (10 units, 037º)
- D. (9 units, 027º)
- Correct Answer: Option A
26. If →PQ = -2i + 5j and →RQ = -i – 7j, find →PR
- A. -3i + 12j
- B. -3i – 12j
- C. -i + 12j
- D. i – 12j27
- Correct Answer: Option C
27. The table shows the distribution of the distance (in km) covered by 40 hunters while hunting.
| Distance(km) | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequency | 5 | 4 | x | 9 | 2x | 1 |
If a hunter is selected at random, find the probability that the hunter covered at least 6km.
- A. 3/5
- B. 2/5
- C. 3/8
- D. 9/40
- Correct Answer: Option A
28. The table shows the distribution of the distance (in km) covered by 40 hunters while hunting.
What is the mode of the distribution?
| Distance(km) | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequency | 5 | 4 | x | 9 | 2x | 1 |
- A. 5
- B. 6
- C. 7
- D. 8
- Correct Answer: Option C
29. If g(x) = √(1-x2), find the domain of g(x)
- A. x < -1 or x > 1
- B. x ≤ -1 or x ≥1
- C. -1 ≤ x ≤ 1
- C. -1 < x < 130
- Correct Answer: Option C
30. Find the coefficient of x3y2 in the binomial expansion of (x-2y)5
- A. -80
- B. 10
- C. 40
- D. 80
- Correct Answer: Option C
31. The first, second and third terms of an exponential sequence (G.P) are (x – 4), (x + 2), and (3x + 1) respectively. Find the values of x.
- A. −1/2,8
- B. 1/2,−8
- C. −1/2,−8
- D. 1/2,8
- Correct Answer: Option A
32. A body of mass 18kg moving with velocity 4ms-1 collides with another body of mass 6kg moving in the opposite direction with velocity 10ms-1. If they stick together after the collision, find their common velocity.
- A. 1/2 m/s
- B. 1/3 m/s
- C. 2m/s
- D. 3m/s33
- Correct Answer: Option A
33. The mean heights of three groups of students consisting of 20, 16 and 14 students each are 1.67m, 1.50m and 1.40m respectively. Find the mean height of all the students.
- A. 1.63m
- B. 1.54m
- C. 1.52m
- D. 1.42m
- Correct Answer: Option A
34. Find correct to the nearest degree, the acute angle formed by the lines y = 2x + 5 and 2y = x – 6
- A. 76o
- B. 53∘
- C. 37∘
- D. 14∘
- Correct Answer: Option C
35. Solve: 4sin2θ + 1 = 2, where 0º < θ < 180º
- A. 60º 0r 120º
- B. 30º 0r 150º
- C. 30º 0r 120º
- D. 60º 0r 150º
- Correct Answer: Option B
36. Find the range of values of x for which 2x2 + 7x – 15 ≥ 0.
- A. x ≤ -5 or x ≥ 3/2
- B. x ≥ -5 or x ≤3/2
- C. -5 ≤ x ≤ 3/5
- D. 3/5 ≤ x ≤ -537
- Correct Answer: Option A
37. The probability that a student will graduate from college is 0.4. If 3 students are selected from the college, what is the probability that at least one student will graduate?
- A. 0.06
- B. 0.22
- C. 0.78
- D. 0.8038
- Correct Answer: Option C
38. The equation of a circle is given as 2x2 + 2y2 – x – 3y – 41 = 0. Find the coordinates of its centre.
- A. (−1/4, 3/4)
- B. (1/4, 3/4)
- C. (−1/2, 3/2)
- D. (−1/2, −3/2)

Correct Answer: Option B
39. The gradient of a function at any point (x,y) 2x – 6. If the function passes through (1,2), find the function.
- A. x2 – 6x – 5
- B. x2 – 6x + 5
- C. x2 – 6x – 3
- D. x2 – 6x + 7
- Correct Answer: Option D
40. A particle of mass 3kg moving along a straight line under the action of a F N, covers a line distance, d, at time, t, such that d = t2 + 3t. Find the magnitude of F at time t.
- A. 0N
- B. 2N
- C. 3(2t + 3)N
- D. 6N
- Correct Answer: Option D
41. If α and β are roots of x2 + mx – n = 0, where m and n are constants, form the
| equation | whose | roots | are | 1 /α | and | 1/ β | . |
- A. mnx2 – n2 x – m = 0
- B. mx2 – nx + 1 = 0
- C. nx2 – mx + 1 = 0
- D. nx2 – mx – 1 = 0
- Correct Answer: Option D
42. A particle is acted upon by forces F = (10N, 060º), P = (15N, 120º) and Q = (12N, 200º). Express the force that will keep the particle in equilibrium in the form xi + yj, where x and y are scalars.
- A. 17.55i + 13.78j
- B. 17.55j – 13.78i
- C. -17.55i + 13.78j
- D. -17.55i – 13.78j43
- Correct Answer: Option B
43. Evaluate: limx→−2 x3+8/x+2
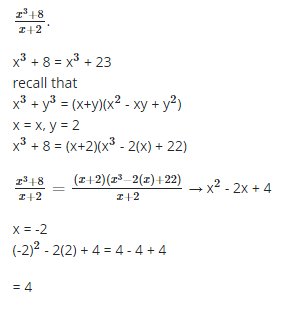
44. If f(x-1) = x3 + 3x2 + 4x – 5, find f(2)
- A. 61
- B. 25
- C. 20
- D. 13
- Correct Answer: Option A
45. The length of the line joining points (x,4) and (-x,3) is 7 units. Find the value of x.
- A. 4√3
- B. 2√6
- C. 3√2
- D. 2√3
- Correct Answer: Option D
More Objective Questions and Answers Loading…
WAEC Further Mathematics Theory Questions 2025
1.
A binary operation * is defined on the set T = {-2,-1,1,2} by p*q = p2 + 2pq – q2, where p,q ∊ T.
Copy and complete the table.
| * | -2 | -1 | 1 | 2 |
| -2 | 7 | -8 | ||
| -1 | 2 | -2 | ||
| 1 | -7 | 1 | ||
| 2 | -1 |
2. Solve 2(2y+1)−5(2y) + 2 = 0
3. Two functions f and g are defined on the set of real numbers, R, by
f:x → x2 + 2 and g:x → 1/x+2.Find the domain of (g∘f)−1
4. Solve 3cos2x – sinx = 0 for 0º≤x≤360º
5. The probability that Abiola will be late to the office on a given day is 2/5. In a given working week of six days, find, correct to four significant figures, the probability that he will:
(a) only be late for 3 days.
(b) not be late in the week:
(c) be late throughout the six days.
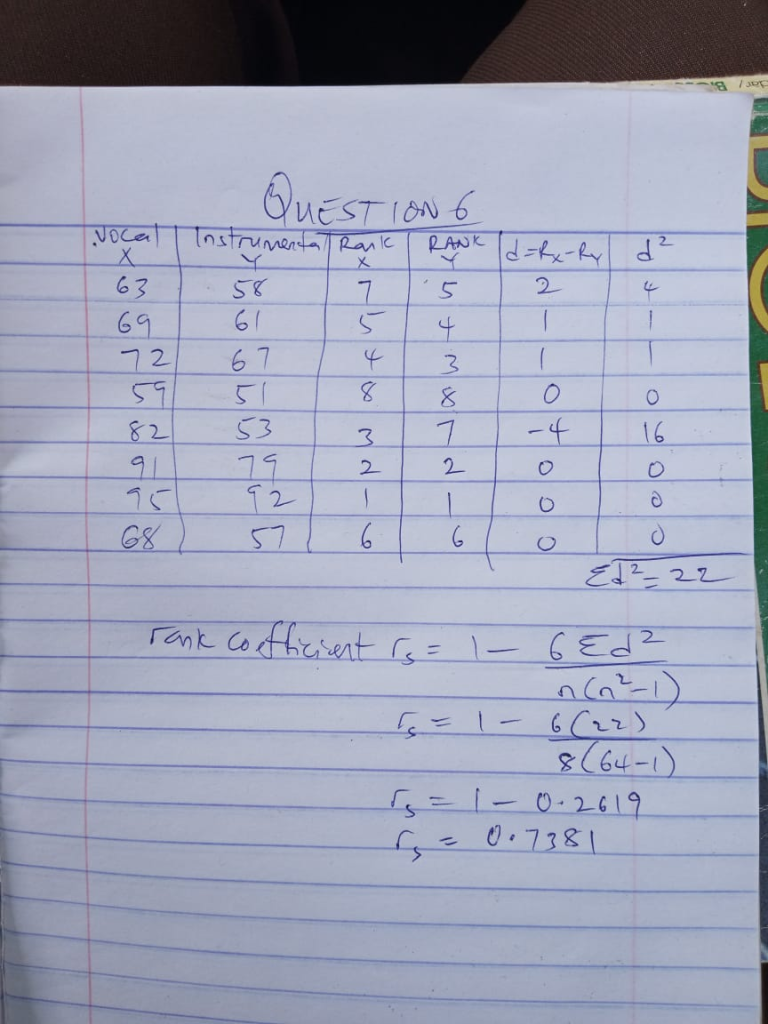
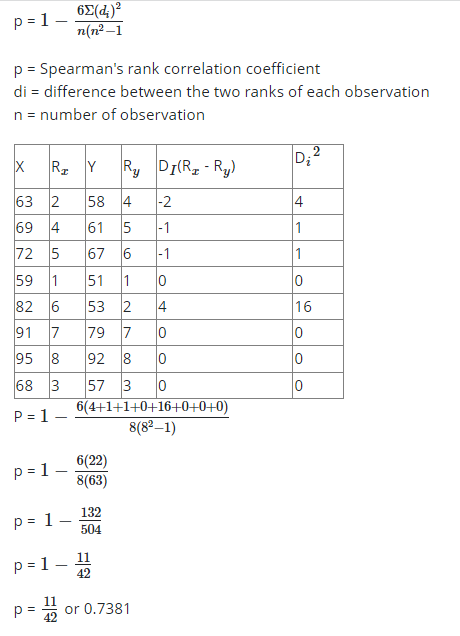
6. The table shows the scores obtained by a group of artistes in Vocal (X) and the instrument (Y) musical competition.
| Vocal (X) | 63 | 69 | 72 | 59 | 82 | 91 | 95 | 68 |
| Instrument (Y) | 58 | 61 | 67 | 51 | 53 | 79 | 92 | 57 |
Calculate the spearman’s rank correlation coefficient between the scores.
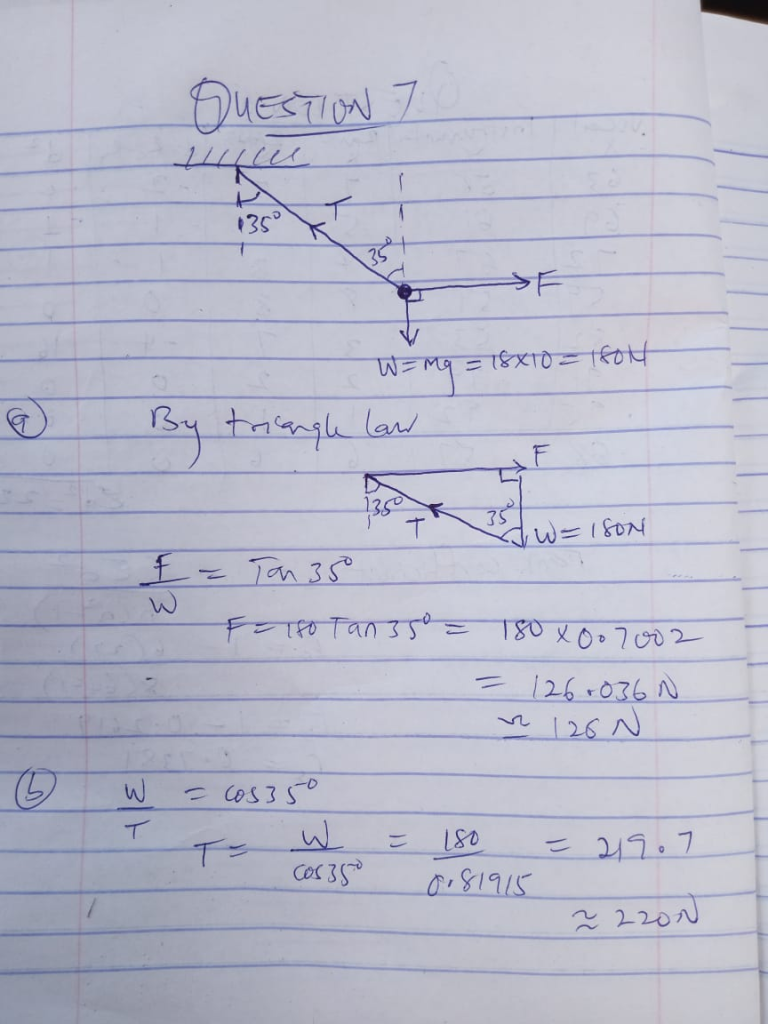
7. A body of mass of 18kg is suspended by an inextensible string from a rigid support and is pulled by a horizontal force F until the angle of inclination of the string to the vertical is 35º. If the system is in equilibrium, calculate the:
i. value of F
ii. tension in the string
8. Given that p = (8N,030º) and q = (9N, 150º), find, in component from, the unit vector along(p – q).
9. Given that nC4, nC5 and nC6 are the terms of a linear sequence (A.P), find the :
i. value of n
ii. common differences of the sequence.
10.
A solid rectangular block has a base that measures 3x cm by 2x cm. The height of the block is ycm and its volume is 72cm3.
i. Express y in terms of x.
ii. An expression for the total surface area of the block in terms of x only;
iii. the value of x for which the total surface area has a stationary value.
11. A basket contains 12 fruits: orange, apple and avocado pear, all of the same size. The number of oranges, apples and avocado pear forms three consecutive integers.
Two fruits are drawn one after the other without replacement. Calculate the probability that:
i. the first is an orange and the second is an avocado pear.
ii.both are of same fruit;
iii. at least one is an apple
12.
The table shows the corresponding values of two variables X and Y.
| X | 14 | 16 | 17 | 18 | 22 | 24 | 27 | 28 | 31 | 33 |
| Y | 22 | 19 | 15 | 13 | 10 | 12 | 3 | 5 | 3 | 2 |
a. plot a scatter diagram to represent the data
b i. Calculate:x̄, the mean of X and ȳ, the mean of Y;
ii. Caculate:
x̄1, the mean of X values below x̄ and ȳ1, the mean of the corresponding Y values below x̄
c. Draw the line of best fit through (x̄,ȳ) and (x̄1,ȳ1).
d. From the graph, determine the relationship between X and Y;
ii. From the graph, determine the value of Y when X is 20.
13.
A particle initially at rest moves in a straight line with an acceleration of (10t – 4t2)m/s2
Find the:
a. velocity of the particle after t seconds;
ii. average acceleration of the particle during the 4th second.
b. A load of mass 120kg is placed on a lift. Calculate the reaction between the floor of the lift and the load when the lift moves upwards at a constant velocity. [Take g = 10m/s2]
ii. with an acceleration of 3m/s2. [Take g = 10m/s2]
14. The vectors 6i + 8j and 8i – 6j are parallel to →OP and →OQ respectively. If the magnitude of →OP and →OQ are 80 units and 120 units respectively, express: →OP and →OQ in terms of i and j;
ii. |→PQ|, in the form c√k, where c and k are constants.
I hope that you are excited with questions you have seen so far.
WAEC Further Mathematics Theory Answers 2025
Now that you have seen the expected theory questions, it is time to show you the correct answers to all the questions. the 2024 Further Mathematics theory answers are as shown below:
1.
p*q = p2 + 2pq – q2
when p = -2 and q = -2
p*q = -22 + 2(-2)(-2) – (-2)2
p*q = 4 + 8 – 4 = 8
when p = -2 and q = -1
p*q = -22 + 2(-2)(-1) – (-1)2
p*q = 4 + 4 – 1 = 7
when p = -2 and q = 1
p*q = -22 + 2(-2)(1) – (1)2
p*q = 4 – 4 -1 = -1
when p = -1 and q = -2
p*q = -12 + 2(-1)(-2) – (-2)2
p*q = 1 + 4 – 4 = 1
when p = -1 and q = -1
p*q = -12 + 2(-1)(-1) – (-1)2
p*q = 1 + 2 -1 = 2
when p = -1 and q = 2
p*q = -12 + 2(-1)(2) – (2)2
p*q = 1 – 4 – 4 = -7
when p = 1 and q = -2
p*q = 12 + 2(1)(-2) – (-2)2
p*q = 1 – 4 – 4 = -7
when p = 1 and q = -1
p*q = 12 + 2(1)(-1) – (-1)2
p*q = 1 – 2 – 1 = -2
when p = 1 and q = 1
p*q = 12 + 2(1)(1) – (1)2
p*q = 1 + 2 – 1 = 2
when p = 1 and q = 2
p*q = 12 + 2(1)(2) – (2)2
p*q = 1 + 4 – 4 = 1
when p = 2 and q = -2
p*q = 22 + 2(2)(-2) – (-2)2
p*q = 4 – 8 – 4 = -8
when p = 2 and q = -1
p*q = 222 + 2(2)(-1) – (-1)22
p*q = 4 – 4 – 1 = -1
when p = 2 and q = 1
p*q = 222+ 2(2)(1) – (1)2
p*q = 4 + 4 – 1 = 7
when p = 2 and q = 2
p*q = 22 + 2(2)(2) – (2)2
p*q = 4 + 8 – 4 = 8
| * | -2 | -1 | 1 | 2 |
| -2 | 8 | 7 | -1 | -8 |
| -1 | 1 | 2 | -2 | -7 |
| 1 | -7 | -2 | 2 | 1 |
| 2 | -8 | -1 | 7 | 8 |
2.
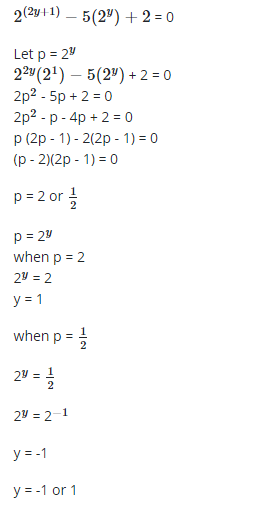
3.

4.
3cos2x – sinx = 0
cos 2A = 1 – 2 sin2A
3(1 – 2sin2x) – sinx = 0
3 – 6sin2x -sinx = 0
let sinx = p
3 – 6p2 -p = 0
-6p2 – p +3 = 0
factors of p in the eqn:
p = 0.7953 or 0.6287
when p = 0.7953
p = sinx
x = sin−1 p
x = sin−1(0.7953)
x = 52.68º
when p = 0.6287
p = sinx
x = sin−1 p
x = sin−1(0.6287)
x = 38.95º
5.
he will be late to office = 2/5
he will not be late to office is = 1 – 2/5 = 3/5
If he will be late for 3 days only, he will also not be late for 3 days
2/5 x 2/5 x 2/5 x 3/5 x 3/5 x 3/5
p = 0.0138
(b) not be late to office is = 1 – 2/5 = 3/5
3/5 x 3/5 x 3/5 x 3/5 x 3×5 x 3/5
p = 0.0467
(c) be late to office = 2/5
2/5 x 2/5 x 2/5 x 2/5 x 2/5 x 2/5
p = 0.0041
6.
7.
If the system is in equilibrium, then the weight of the body = the force pulling it
and the force = the vertical component of force F
since Force F is inclined to vertical then the vertical component = Fcos35º
the weight of the body = mg
Fcos35º = 18(10)
0.8192F = 180
F = 180/0.8192
F = 219.7N
tension in the string
T = mg
T = 18kg × 10
T = 180N
8.
p = 8cos30i + 8sin30j
q = 9cos150i + 9sin150j
p = 6.9282i + 4j
q = -7.7942i + 4.5j
pq = (-7.7942 – 6.9282)i + (4.5 – 4)j
pq = -14.7224i + 0.5j
|pq| = √((-14.7224)2 + (0.5)2)
|pq| = √(216.7491 + 0.25)
|pq| = √216.9991
|pq| = 14.7309
the unit vector in the direction of p – q =
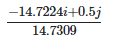
-0.9994i + 0.0339j ≌ -i + 0.0339j
9.

multiply both sides by 5! * 6
6(n-9) = (n-4)(n-11)
6n – 54 = n2 -11n – 4n + 44
6n – 54 = n2 – 15n + 44
n2 – 21n + 98 = 0
n2 – 7n – 14n + 98 = 0
n(n – 7) -14(n – 7) = 0
(n-7)(n-14) = 0
n = 7 or 14
10.
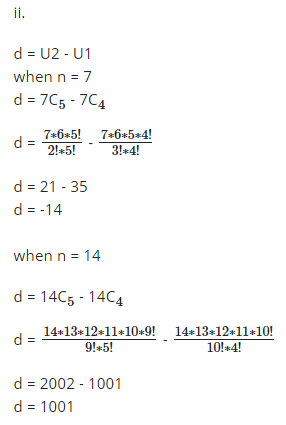
Continuation of Theory Answers
12.
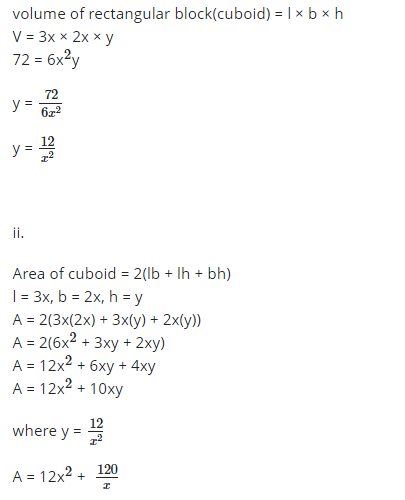
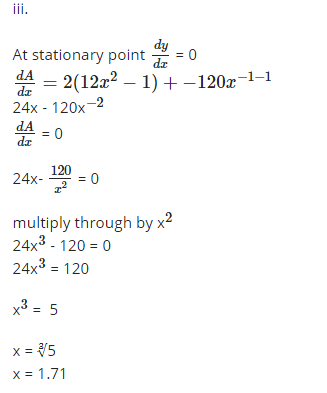
13.

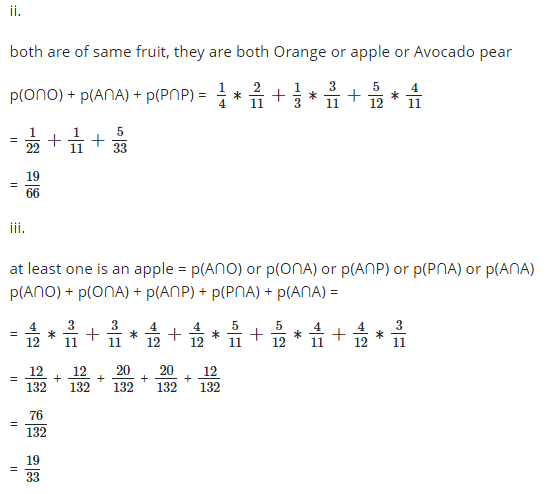
15.
a. a = (10t – 4t2)m/s2, t = t seconds, u = 0
from first equation of motion,
v = u + at
v = 0 + (10t – 4t2)t
v = (10t2 – 4t3)m/s2
ii. average acceleration of the particle during the 4th second = the average acceleration between the t = 3 and t = 4
Δa4 = 10(t4-t3) – 4(t4-t3)2
Δa4 = 10(4-1) – 4(4-3)2
Δa4 = 10(1) – 4(12)
Δa4 = (10-4)m/s2
Δa4 = 6ms-2
b. R = m(g+a)
When the lift moves with a constant velocity, a = 0
R = mg
R = 120 × 10
R = 1200N
ii. when the lift moves upward with an acceleration of 3m/s2
R = m(g+a)
R = 120(10+3)
R = 120 × 13
R = 1560N
Recommended Posts:
WAEC English Questions And Answers 2025 | Objectives, Test Of Orals and Essay
WAEC Government Questions and Answers 2025 | Essay & Objective
WAEC Economics Questions And Answers 2025 | Theories And Objectives
WAEC Commerce Questions and Answers 2025 | Essay & Objectives
WAEC Marketing Questions And Answers 2025 | Essay & Objectives
WAEC French Questions And Answers 2025 | Theories And Objectives
WAEC Mathematics Questions And Answers 2025 | Theory And Objectives
I hope you are satisfied with the information that you have seen in this article. In case of any other questions about WAEC Further Mathematics Questions and Answers 2025, kindly make use of the comment section on this page.
Do well to share this article with others
